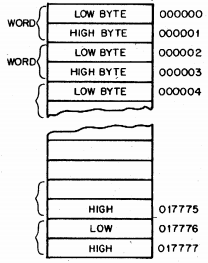
Like many other computer systems created in the 1960s, all PDP-11 literature expresses numbers in octal notation. Each octal digit is made up of three bits, expressing 0 through 7. In this notation, a byte value (8 bits) ranges from 000 to 377, and a word value (16 bits) ranges from 000000 to 177777. This is physically expressed in the PDP-11 console, which groups its switches and lights into threes, making it easier to enter and display numeric values using switches and lights.

16-bit values can be interpreted as "unsigned" or "signed", depending on the instructions that use the value. The most significant bit can be interpreted as the sign: unset indicates the value is positive, set indicates the value is negative. If the value is unsigned, 000000 represents zero, and 177777 represents the decimal value 65535. If the value is considered to be signed, the PDP-11 interprets the value using "twos' compliment": to negate a number, the bits are inverted, and one is added. In this case, 000000 still represents zero, and 177777 represents negative one. In twos' compliment notation, positive ten is represented as 000012 (octal, of course), and negative ten is the negation of 000012, which is 177765, plus one, leaving us with 177766. Notice that applying the twos' compliment algorithm again gives us the original value: negating 177766 gives 000011, plus one gives 000012. Nearly all modern computers still use twos' compliment notation for signed values.

In memory, the PDP-11 stores the individual bytes of a word in "little- endian" order. For example, if the word at memory location 1000 contains the word value 125063 (octal, of course), then location 1000 contains the lowest eight bits 063, and location 1001 contains the higest eight bits 252.